After reading this article in FSM, I decided to have a go at doing fractal images with Octave. In the process, I discovered quite a bit about fractals so here is the result of those experiments. First I'll build some classic Mandelbrot and Julia fractal images.
Pre-Requisites
All the code below was created on Ubuntu using Octave. If you don't use Ubuntu, check with your distribution or follow the instructions on the Octave web site. If you have Ubuntu, you just need to install the Octave package. To do this, open a terminal and type the following at the command line:
$ sudo apt-get install octave
Alternatively, considering that Octave is meant to be compatible with MATLAB, it should be possible to adapt everything in this series to MATLAB.
Fractal Basics
Fractals is a term that encompasses a variety of mathematical constructions that all have a property in common: they are inherently recursive. This means that you can only ever produce an approximation of a fractal to a given level of precision, which is why their study is well adapted to computational approximation methods, what a computer is inherently designed for.
Mandelbrot and Julia sets are generated as a result of studying the convergence properties of series in the complex plane. The series that is most commonly used is:
zn+1=zn2+c
This series converges or diverges for large values of n, depending on the value of z0 and c. All well and good but how does that help us produce cool fractal images with Octave? We're getting there.
The Julia and Mandelbrot sets
The Julia sets (from Gaston Julia who first studied such series) show the behaviour of complex series when you vary the value of z0 in the complex plane, for a given value of c. But the question is then: what are interesting values of c?
Conversely, the Mandelbrot sets (from Benoît Mandelbrot who first used a computer to study such series) show the behaviour of the same series when you vary the value of c in the complex plane, for a given value of z0, the most classic example using z0=0.
Constructing an Image
So, if we map the pixels of our image to the complex plane, we can associate a value of c to each pixel and calculates values of zn for z0=0 in order to obtain a Mandelbrot image.
But what values of n are we interested in and what do we do with the value we calculate? As said above, we are interested in whether the series diverges or not so we could colour a pixel in white if it diverges and in black if it converges.
How do we know whether the series converges or diverges then? Some people much smarter than I am have proven that for a given polynomial series, there exists a value r such that if for any n, |zn|>r, then the series diverges. For the polynomial given above, r=2.
So now, we can identify for each point whether the series diverges or converges so we can colour the corresponding pixel white or black. But most Mandelbrot images you see in the wild are not black and white, they are rather colourful: so how do they get all their funky colours? Each colour is associated with how quickly the series diverges. To obtain that effect, we will associate the value 0 with points that converge and a number greater than 0 for points that diverge. That number will be the lowest value of n for which |zn|>r. Each value will then be associated to a colour in a colour to produce the final image.
The Code
After all this background, it's time to do some coding. But first, we need to ensure that Octave knows where to find the functions we will define. The way Octave works, it looks for function files in its path and expects each function to be stored in a file of the same name with the .m suffix. By default, the Octave path doesn't include any directory for which you have write access so what I did was to create an octave directory in my home directory as well as a .octaverc file that adds ~/octave to the path:
From now on, every .m file in the ~/octave directory will be found by Octave and recognised as a function file. You will need to restart Octave for this to take effect.
Now that the preamble is out of the way, we can start coding in earnest so let's fire a trusty file editor and create a file called mandelbrot.m in the ~/octave directory. In this file, we are going to define a mandelbrot function that takes 4 arguments: cmin, cmax, hpx and niter, corresponding respectively to the minimum and maximum values of c, the number of horizontal pixels in the image and the number of iterations:
function M=mandelbrot(cmin,cmax,hpx,niter)
The aim of this function will be to populate the matrix M with the colour values of pixels. The first thing we do is calculate the vertical number of pixels such that ratio of the final picture is the same as the one given implicitly by cmin and cmax:
vpx=round(hpx*abs(imag(cmax-cmin)/real(cmax-cmin)));
We then initialise z, c and M. z and M are easy as they just need to be initialised to zeroes. However, note that the vertical dimension is the first one because Octave orders a matrix per columns first. c is a bit more complicated as it need to be initialised to a matrix that is vpx by hpx in size with real values spread along the horizontal axis and imaginary values spread along the vertical axis. The linspace function produces a vector of values evenly spread between the minimum and maximum across the given number of points. The meshgrid function then produces 2 real matrices out of those 2 vectors that are then merged together as a complex matrix.
z=zeros(vpx,hpx);
[cRe,cIm]=meshgrid(linspace(real(cmin),real(cmax),hpx),
linspace(imag(cmin),imag(cmax),vpx));
c=cRe+i*cIm;
M=zeros(vpx,hpx);
The final part of the function is the main loop. Here we use Octave's full potential using matrix calculation and a matrix mask. The mask is calculated so that it contains all the points that have not yet diverged and the corresponding entries in the result matrix are incremented. Points that diverge are not incremented and are excluded from the next calculation. Finally, we set the remaining points, that is the ones that haven't diverged after niter iterations, to 0.
for s=1:niter
mask=abs(z)<2;
M(mask)=M(mask)+1;
z(mask)=z(mask).^2+c(mask);
endfor
M(mask)=0;
Putting it all together, here is the final file:
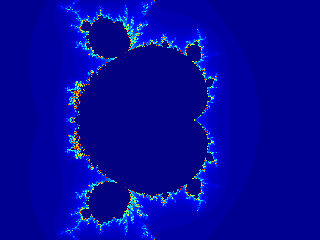
So let's run it to see what comes out of it:
octave-3.0.1:1> Mc=mandelbrot(-2.1+1.05i,0.7-1.05i,640,64);
octave-3.0.1:2> imagesc(Mc)
Octave should then fire up Gnuplot and show a nice classic Mandelbrot set:
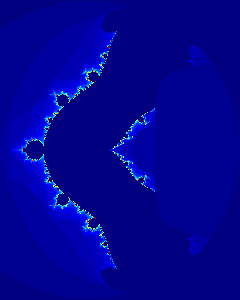
Following this success, let's tackle the Julia set. The code should be very similar, with the exception that c should be a parameter of the function and z is the variable that needs initialisation using linspace and meshgrid. Furthermore, c doesn't need to be masked in the loop because it is a scalar value, not a matrix. So without further ado, here's the code for the ~octave/julia.m file:
Let's choose a value for c that corresponds to a point at the limit of convergence in the Mandelbrot set, such as -0.75+0.2i, and call the julia function:
octave-3.0.1:3> Jc1=julia(-1.6+1.2i,1.6-1.2i,640,64,-0.75+0.2i);
octave-3.0.1:4> imagesc(Jc1)
Octave should then refresh the Gnuplot windows and show the result:
Factorising Code
Considering both function are so similar, it should be possible to factorise code between them and have a core Mandelbrot/Julia function called by two simpler functions. The major difference is in the initialisation before the loop so can we factorise the loop? The only difference in the loop between the two functions is that in the mandelbrot function, c is masked because it is a matrix, whereas in the julia function, it is is not masked because it is a scalar. The solution is to transform c into a matrix of identical values in the julia function. We now have three files: mjcore.m that contains the core code and refactored mandelbrot.m and julia.m. Here is the full listing:
Next
In the next article of this series, More on the Classic Sets, we wander around the Mandelbrot and Julia sets and see what happens to the Mandelbrot set when we choose a value for z0 that is different from 0. I also demonstrate how to save images to disk and talk about colour maps.