The story so far
In this fourth instalment of this series on fractals with Octave, I'll have a look at the Mandelbrot and Julia sets generated by non-polynomial series. Polynomials are fine but they can be a bit boring so what about introducing a sine or exponential in the mix? The original idea for this came from an excellent set of articles and examples by Paul Bourke.
Sine function
The first series we will use is defined thus:
zn+1=c sin(zn)
That's simple enough and very easy to code in Octave so as our mandelbrot and julia functions now have the ability to take a generating series as argument, it should be no problem. But before doing that, we need to know what value to give to r so that we know when the series diverges and when we can stop iterating. In the very first article, we saw that:
[...] for a given polynomial series, there exists a value r such that if for any n, |zn|>r, then the series diverges.
This only applies to polynomials. The series above is not a polynomial series and its condition for divergence is that the imaginary part of zn be greater than 50. That doesn't work well with our current code that expects a simple integer. We could replace the integer parameter expected by the mandelbrot and julia functions with a function handle but that would make their usage more complex when using polynomial series. Luckily, we can have the best of both worlds because Octave uses a weakly typed language: the type of a parameter passed to a function is not specified in the function definition, meaning that you can pass anything, you just have to hope that it is what the function expects. While this can be seen as a drawback for long and complex programs where validation can be cumbersome, it is actually a useful feature for a high level language like Octave where functions tend to be short. To make it work, we need to modify the mjcore function so that it can accept a function handle or an integer as its fifth parameter and act accordingly. For this, we will use the Octave isa built-in function to identify whether the parameter is a function handle. Here's how to modify the mjcore function:
mjcore.m
function M=mjcore(z,c,niter,f,r)
if(isa(r,"function_handle"))
rf=r;
else
rf=@(z) abs(z)<r;
endif
M=zeros(length(z(:,1)),length(z(1,:)));
for s=1:niter
mask=abs(z)<rrf(z);
M(mask)=M(mask)+1;
z(mask)=f(z(mask),c(mask));
endfor
M(mask)=0;
endfunction
That's all great and now we should be able to create our first sine Mandelbrot. We need to make sure that we reverse the comparison operator in the last parameter because our code is built so that we provide a convergence condition rather than a divergence one:
octave-3.0.1:1> Msin=mandelbrot(-1.2*pi+0.9*pi*i,1.2*pi-0.9*pi*i, > 320,64, > @(z,c) c.*sin(z), @(z) abs(imag(z))<=50); octave-3.0.1:2> imagesc(Msin)
And we end up with... a dark blue rectangle, not quite what was expected. This is because in this form, the value of z0 is 0, therefore sin(z0) is also 0 and so is c sin(z0): the series is always null and never diverges. To correct this, we would need to have z0=c, that is initialise the series to the values of c. But if we do that in the code of the mandelbrot function, it will break some of our previous examples. That is unless we can specify a special value of z0 to the mandelbrot function to force it to initialise to z0=c. A similar trick to what we did for r above can do that: if the given parameter is the special string "c", initialise to c, otherwise assume the parameter is an integer and initialise as before. Here is the modified mandelbrot function:
mandelbrot.m
function M=mandelbrot(cmin,cmax,hpx,niter,
f=@(z,c) z.^2.+c,r=2,
z0=0)
vpx=round(hpx*abs(imag(cmax-cmin)/real(cmax-cmin)));
z=zeros(vpx,hpx).+z0;
[cRe,cIm]=meshgrid(linspace(real(cmin),real(cmax),hpx),
linspace(imag(cmin),imag(cmax),vpx));
c=cRe+i*cIm;
if(strcmp("c",z0))
z=c;
else
z=zeros(vpx,hpx).+z0;
endif
M=mjcore(z,c,niter,f,r);
endfunction
After that modification, we can run the mandelbrot function again with our new special parameter:
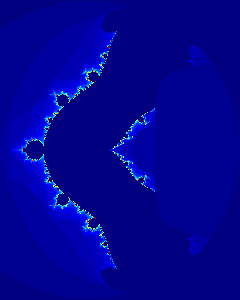
octave-3.0.1:1> Msin=mandelbrot(-1.2*pi+0.9*pi*i,1.2*pi-0.9*pi*i, > 320,64, > @(z,c) c.*sin(z), @(z) abs(imag(z))<=50, "c"); octave-3.0.1:2> imagesc(Msin)
Octave should open the Gnuplot window and display an image similar to this:
We can also generate a sine Julia set without any change to the julia function:
octave-3.0.1:1> Jsin=julia(-2.4*pi+1.8*pi*i,2.4*pi-1.8*pi*i, > 320,64,1+0.5i, > @(z,c) c.*sin(z), @(z) abs(imag(z))<=50); octave-3.0.1:2> imagesc(Jsin)
Cool stuff! So let's have a look at other non-polynomial functions and their output.
Cosine
This series is defined by:
zn+1=i c cos(zn)
And has the same convergence condition than the previous series.
octave-3.0.1:1> Mcos=mandelbrot(-1.2*pi+0.9*pi*i,1.2*pi-0.9*pi*i, > 320,64, > @(z,c) i.*c.*cos(z), @(z) abs(imag(z))<=50, "c"); octave-3.0.1:2> imagesc(Mcos)
octave-3.0.1:1> Jcos=julia(-2.4*pi+1.8*pi*i,2.4*pi-1.8*pi*i, > 320,64,0.55+1.195i, > @(z,c) i.*c.*cos(z), @(z) abs(imag(z))<=50); octave-3.0.1:2> imagesc(Jcos)
Tangent
This series is defined by:
zn+1=c tan(zn)
And uses the same convergence function as a polynomial with the default value of r.
octave-3.0.1:1> Mtan=mandelbrot(-1.4+1.4i,1.4-1.4i, > 320,64, > @(z,c) c.*tan(z), :, "c"); octave-3.0.1:2> imagesc(Mtan)
octave-3.0.1:1> Jtan=julia(-1.4+1.4i,1.4-1.4i, > 320,64,(1+i)*sqrt(2)/2, > @(z,c) c.*tan(z)); octave-3.0.1:2> imagesc(Jtan)
Exponential
First, let's multiply the exponential using the following series:
zn+1=c exp(zn2)
This series uses the default values for r and z0.
octave-3.0.1:1> Mexp1=mandelbrot(-1.4+2i,1.4-2i, > 240,64, > @(z,c) c.*exp(z.^2)); octave-3.0.1:2> imagesc(Mexp1)
Then, let's add to the exponential using the following series:
zn+1=exp(zn2)+c
This series also uses the default values for r and z0.
octave-3.0.1:1> Mexp2=mandelbrot(-2.2+2i,1-2i, > 240,64, > @(z,c) exp(z.^2).+c); octave-3.0.1:2> imagesc(Mexp2)
Cactus
Finally, let's draw a cactus using the following series:
zn+1=zn3+(z0-1)zn-z0
This series uses the default values for r and the special value z0=c.
octave-3.0.1:1> Mcactus=mandelbrot(-0.8+0.6i,0.8-0.6i, > 320,64, > @(z,c) z.^3.+(c.-1).*z.-c,:,"c"); octave-3.0.1:2> imagesc(Mcactus)
Next
Next in this series, we will look at a fractal called the Burning Ship.








1 comment:
Whoa, dude. Totally beyond me...
yet not only is it possible for you
to achieve 7thHeaven, but sHe
wants you instruct us Upstairs
on finer points, dude-withe-lude.
Follow me to the WeddingFeast:
● NOPEcantELOPE.blogspot.com ●
Excuse-moi, aussi, s'il-vous plait:
● en.gravatar.com/MatteBlk ●
Post a Comment